Rewind, painfully perhaps, to May 2020. We didn't know it at the time - we barely knew anything - but we'd just passed the nadir of the COVID impact in your offices. I was freaking out, wondering what would happen to pediatric offices after another month of no visits. Paulie and I were locked in every Thursday night trying to figure it out.

One of the predictions I made, in a fit of optimism, was that we'd see a baby boom in 9-12m as a result of the lockdown. I'd forgotten about that consideration until a note on the PMI forum reminded me to look into it.

Measuring for the implication of a birth rate difference is tricky for a couple reasons. First, although PCC has national and demographic spread, newborn volume isn't like, say, E&M codes. We also don't have actual birth data, just the appearance of new babies in our client offices. Finally, I'd like to start paying more attention to the differences that occur in the Medicaid population. But all that for later - here's what we did!

We can't simply count 99381s over time - not every practice bills 99381s, which would make this exercise a lot easier. The problem with counting 99391s, of course, is that a newborn should have 5-7 99391s in the first year of life. Although we could presume that an increase in 99391s reflects an increase in births, there are too many other variables affecting visit volumes over this time frame for us to fully trust that.

What we came up with is to look for the first 99391 for each unique patient and count them as being a newborn in that month. YES, it means that if a 9mo shows up at a practice for the first time, having been seen elsewhere, they'll count as a newborn. But we're using the same ruleset for pre- and post-COVID and we have no reason to believe movement like that is a) particularly common and b) different now vs. 2020.

The results are fascinating. I know most of you just scrolled down to the pictures, so here it is:

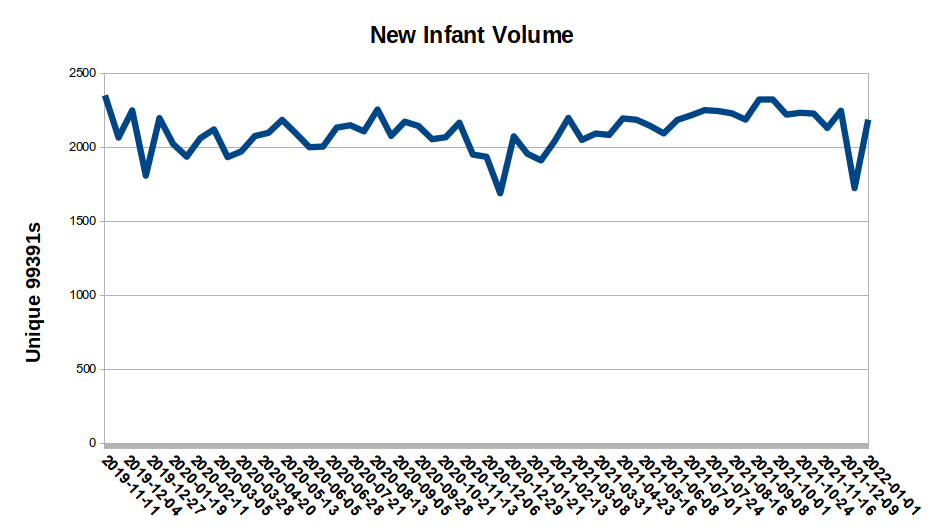
We've counted those "unique" 99391s for all the practices who were with us for the entire time period (essentially, November 2019 through December 2021).  Visually, the baby bump appears to be there.  You'll first notice the 3 "Christmas/New Years" dips that occur every year, but you can see the bump clearly starting in March 2021, 1 year after COVID hit (and roughly 8-10m after most of the US really hit lockdown). But can we PROVE that there is a difference? I was also concerned that the different bin-size decisions I was making could color the results (1 week samples, 2 week samples, monthly?, etc.).

I was scratching my head for a bit when I realized I have a special resource. One of my offspring, The Nudge, is doing healthcare focused analytical work, so I called him. "Just do a paired-T test with the two time periods." I could feel the rust and cobwebs falling away from my confused mind. Oh yes! I grabbed the volume data from February 2020 through Dec 2020 and compared it to the same time period in 2021 [they were offset by a single week and grouped into biweekly segments]. The results are, I believe, unequivocal - it's extremely statistically significant (t-stat of -6.2) that those two time frames represent different volumes of 99391s.  The difference is about 5% of increased monthly volume, so it's not a massive number, but it's real.  We can also say that the rate of baby-making hasn't appeared to slow, yet, as a result of the pandemic, but there's always at least a 9-12 month delay required to review the data.

One could argue that 2020 was more likely to reflect a family having NO 99391s as a result of not coming into the practice for COVID reasons- technically true and I am sure it happened, but not at a volume that affects these results.

Note this news: Maternity wards are shuttering across the US during the pandemic.  Another reason to study the impact of information like this on different patient populations.

[I might look at a correlation between 99381 volume and this data as well as overall 99391 volume - it'd be good to know if there's a simpler way to measure.]